Excel 2010 mátrix szorzás (MMULT)

Korábban már ismertettük, hogyan lehet a mátrix inverzét értékelni. Most az Excel-t fogjuk használni MMULT funkció a mátrix közvetlen szorzásának megismerésére, ahelyett, hogy manuálisan fogalmazna meg. Az adatértékek tömbként is foglalkozik, és tömböt fogad argumentumként.

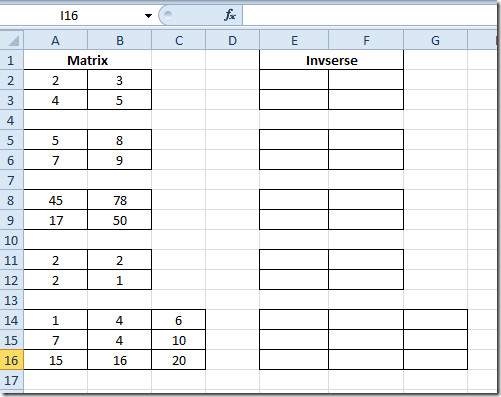
Indítsa el az Excel 2010 táblázatot, amelyen meg kell találnia a mátrix szorzását. Például egy táblát tartalmazott, amely mezőket tartalmaz; Matrix1, Matrix2 és Szorzás amint az az alábbi képernyőképen látható.

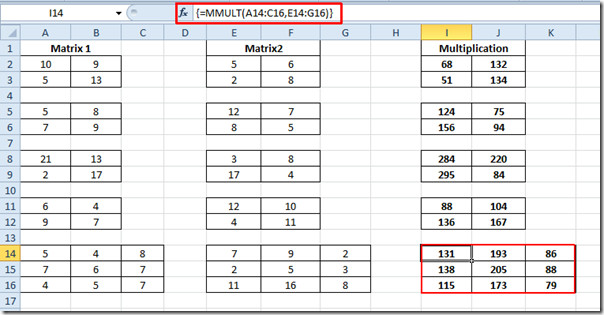
Meg fogjuk találni a szorzótmátrixok. Három 2 × 2 és egy 3 × 3 mátrixunk van. A képlet minden kategóriánál teljesen azonos lenne. A szorzás kiértékelésének régi módszere nagyon hosszú lehet, különösen akkor, ha 3x3-as mátrixgal kell foglalkoznunk. De az MMULT függvényt fogjuk használni. Ennek a függvénynek a szintaxisa;

A függvény első és második érve:egy egyszerű tömb, mivel argumentumként tömböt vesz fel, és a cellának a helyét fogjuk meghatározni, ahol a tömb található. De az értékeket közvetlenül is megadhatja.

Ezt a függvényt a következőképpen írjuk:

Mint A2:B3 a cella azon helye, ahol az első mátrixunk tartózkodik, és E2: F3 a második helye. Mivel itt a tömbtel foglalkoztunk, ezért a Ctrl + Shift + Enter billentyűkombinációval be kell zárni a függvényt göndör zárójelben, ami a tömbök használatát jelzi.

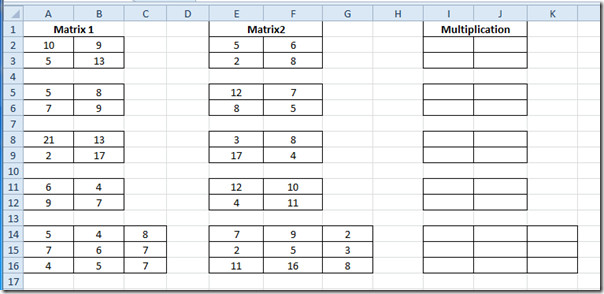
Most válassza ki az első mátrixcellákat Szorzás mezőbe, és csak írja be a függvényt a fent említettek szerint. A kapott szorzási eredmény 4 sejt lesz, ahogy a 2x2-es mátrixot vizsgáltuk.

A szorzás eredményeinek megismerésére másmátrixokat, válassza ki az értékelt mátrixot, és csak másolja be és illessze be más 2 × 2 mátrixokba. Amint az alább látható, hogy a mátrixot éppen alatta mátrixba másoltuk.

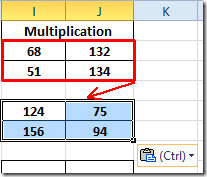
Most ismételje meg ugyanazt az eljárást az összes 2 × 2 mátrixra. 3 × 3 mátrix esetén írja le újra a függvényt, megadva minden cellának a helyét mindkét mátrixban.

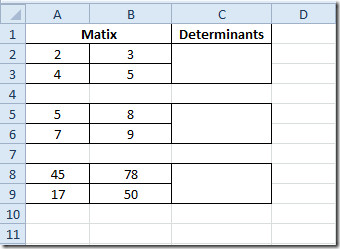
Ellenőrizheti a korábban áttekintett Mátrix működési funkciót is; A mátrix determináns (MDETERM) kiértékelése és a mátrix inverzének kiderítése.