„Excel 2010“ matricos daugyba (MMULT)

Anksčiau mes aptarėme, kaip įvertinti matricos atvirkštinę vertę. Dabar mes naudosime „Excel“ būdingą MMULT funkcija, norint sužinoti matricos dauginimą tiesiogiai, o ne formuojant rankiniu būdu. Čia taip pat nagrinėjamos duomenų vertės kaip masyvas ir masyvas laikomas kaip argumentas (-ai).

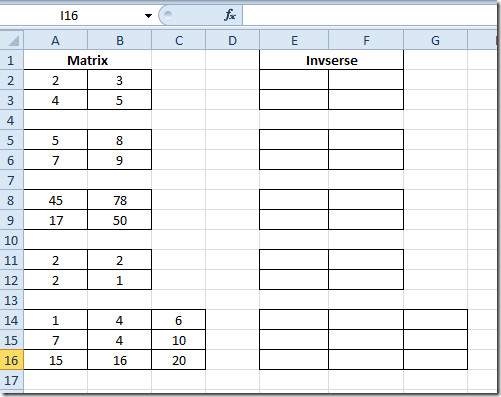
Paleiskite „Excel 2010“ skaičiuoklę, kurioje turite sužinoti matricos daugybą. Pavyzdžiui, mes įtraukėme skaičiuoklę, kurioje yra laukai; „Matrix1“, „Matrix2“ ir Daugyba kaip parodyta paveikslėlyje žemiau.

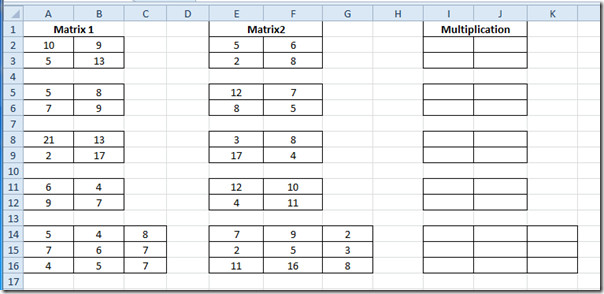
Mes išsiaiškinsime dauginimąsimatricos. Mes turime tris 2 × 2 ir vieną 3 × 3 matricą. Kiekvienai kategorijai formulė būtų visiškai vienoda. Senasis daugybos įvertinimo metodas gali būti labai ilgas, ypač kai turime susitvarkyti su 3 × 3 matrica. Bet mes naudosime MMULT funkciją. Pagrindinė šių funkcijų sintaksė yra;

Pirmasis ir antrasis funkcijos argumentas yrapaprastas masyvas, kadangi masyvas laikomas argumentu, pateikdami langelio vietą ten, kur gyvena masyvas. Tačiau vertybes taip pat galite įvesti tiesiogiai.

Parašysime šią funkciją kaip;

Kaip A2:B3 yra ląstelės, kurioje yra mūsų pirmoji matrica, vieta, o E2: F3 yra antrosios. Kadangi čia buvo kalbama apie masyvą, todėl jums reikia paspausti „Ctrl“ + „Shift“ + „Enter“, kad funkcija būtų įtraukta į skliaustelius, kurie nurodo masyvų naudojimą.

Dabar pasirinkite pirmąsias matricos langelius Daugyba lauką ir tiesiog įveskite funkciją, kaip minėta aukščiau. Tai suteiks dauginimo rezultatą 4 ląstelėse, nes mes įvertinome 2 × 2 matricą.

Norėdami sužinoti daugybos rezultatus kitosematricas, pasirinkite įvertintą matricą ir tiesiog nukopijuokite ir įklijuokite į kitas 2 × 2 matricas. Kaip parodyta žemiau, mes ką tik nukopijavome matricą į matricą, esančią po ja.

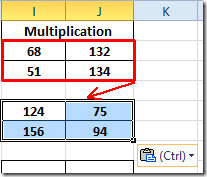
Dabar pakartokite tą pačią procedūrą visoms 2 × 2 matricoms. 3 × 3 matricai užrašykite funkciją dar kartą, nurodydami kiekvienos ląstelės vietą abiejose matricose.

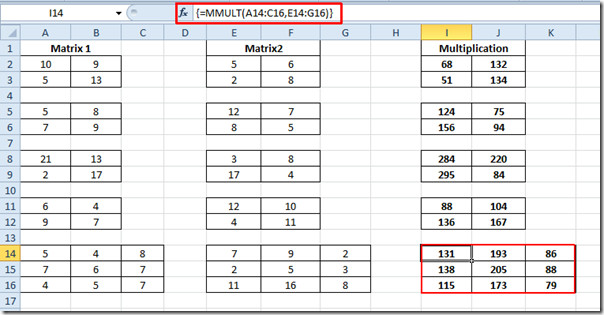
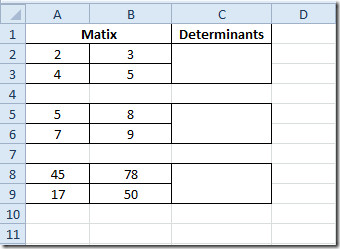
Taip pat galite patikrinti anksčiau peržiūrėtą „Matrix“ funkcijos funkciją; Įvertinti matricos determinantą (MDETERM) ir sužinoti matricos atvirkštę.