Excel 2010 matricas reizināšana (MMULT)

Iepriekš mēs apskatījām, kā novērtēt matricas apgriezto vērtību. Tagad mēs izmantosim Excel raksturīgo MMULT funkcija, lai uzzinātu matricas reizināšanu tieši, nevis dodoties uz manuālu formulēšanu. Tajā ir aplūkotas arī datu vērtības kā masīvs un masīvs tiek ņemts vērā kā arguments (-i).

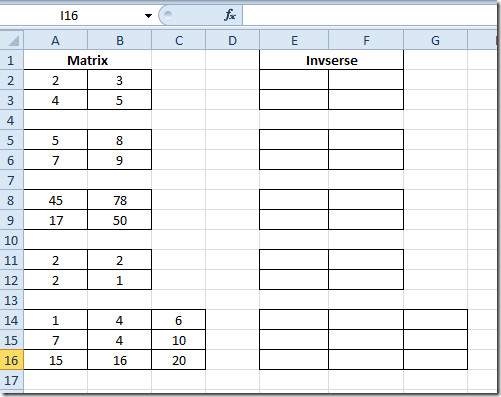
Palaidiet Excel 2010 izklājlapu, kurā jāatrod matricas reizināšana. Piemēram, mēs esam iekļāvuši izklājlapu, kurā ir lauki; Matrix1, Matrix2 un Reizināšana kā parādīts zemāk esošajā ekrānuzņēmumā.

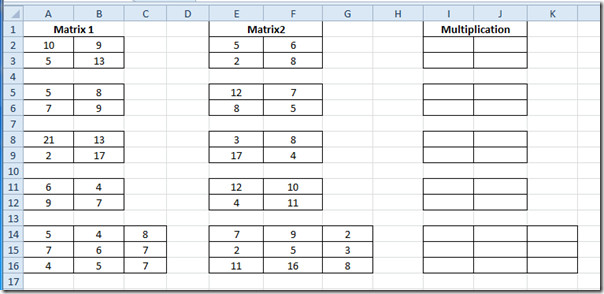
Mēs uzzināsim, kā reizinātmatricas. Mums ir trīs 2 × 2 un viena 3 × 3 matrica. Katrai kategorijai formula būtu absolūti vienāda. Vecā reizināšanas novērtēšanas metode varētu būt ļoti gara, it īpaši, ja mums ir jātiek galā ar 3 × 3 matricu. Bet mēs izmantosim MMULT funkciju. Šīs funkcijas pamata sintakse ir;

Funkcijas pirmais un otrais arguments ir:vienkāršs masīvs, jo masīvs tiek uzskatīts par argumentu, un mēs norādīsim šūnas atrašanās vietu, kurā masīvs atrodas. Tomēr vērtības var ievietot arī tieši.

Mēs šo funkciju uzrakstīsim kā;

Kā A2:B3 ir šūnas atrašanās vieta, kur atrodas mūsu pirmā matrica, un E2: F3 ir otrās atrašanās vieta. Tā kā šeit mēs nodarbojāmies ar masīvu, jums jānospiež Ctrl + Shift + Enter, lai pievienotu funkciju cirtaini iekavās, kas norāda masīvu izmantošanu.

Tagad atlasiet pirmās matricas šūnas Reizināšana laukā un vienkārši ievadiet funkciju, kā minēts iepriekš. Tas dos reizināšanas rezultātu 4 šūnās, jo mēs esam novērtējuši 2 × 2 matricu.

Lai uzzinātu reizināšanas rezultātus citosmatricas, atlasiet novērtēto matricu un vienkārši nokopējiet un ielīmējiet citās 2 × 2 matricās. Kā parādīts zemāk, ka mēs tikko esam kopējuši matricu matricā zem tā.

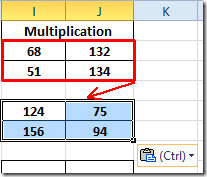
Tagad atkārtojiet to pašu procedūru visām 2 × 2 matricām. 3 × 3 matricai vēlreiz pierakstiet funkciju, nodrošinot katras šūnas atrašanās vietu abās matricās.

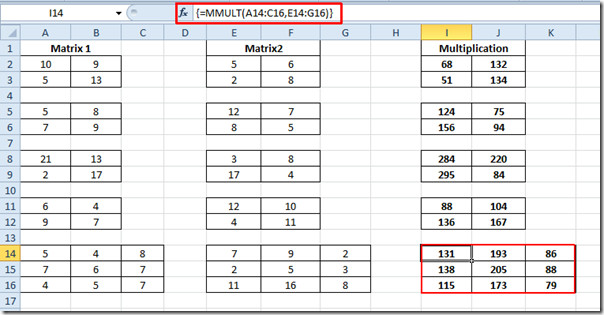
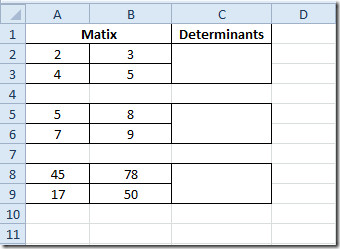
Varat arī pārbaudīt iepriekš pārskatīto Matrix darbības funkciju; Matricas determinanta (MDETERM) novērtēšana un matricas inversijas noskaidrošana.