Excel 2010 Matrix Multiplikation (MMULT)

Tidligere har vi dekket hvordan vi kan evaluere inverse av matrise. Nå skal vi bruke Excel iboende MMULT funksjon for å finne ut multiplikasjon av matrise direkte, i stedet for å gå for manuell formulering. Den omhandler også dataverdier som matrise og tar matrise som argument (er).

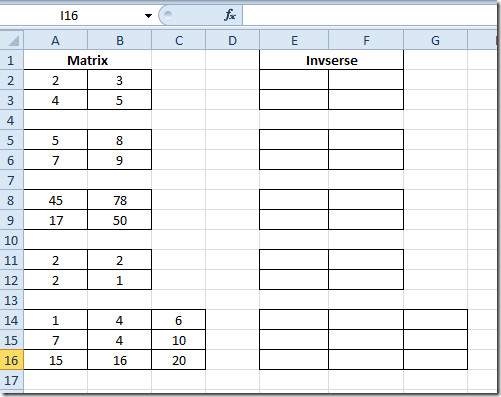
Start Excel 2010-regnearket du trenger for å finne ut matrisenes multiplikasjon. For eksempel har vi tatt med et regneark som inneholder felt; Matrix1, Matrix2 og multiplikasjon som vist på skjermdumpen nedenfor.

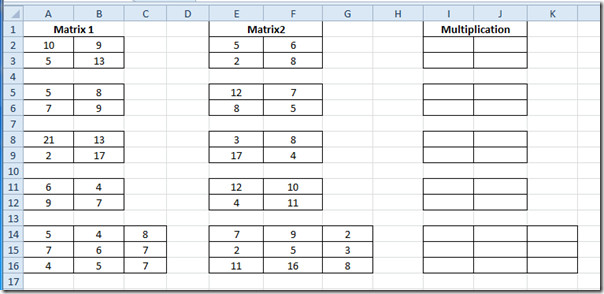
Vi skal finne ut multiplikasjonen avmatriser. Vi har tre 2 × 2 og en 3 × 3 matrise. Formelen vil være absolutt den samme for hver kategori. Den gamle metoden for å evaluere multiplikasjon kan være veldig lang, spesielt når vi har å gjøre med 3 × 3-matrise. Men vi bruker MMULT-funksjon. Den grunnleggende syntaks for disse funksjonene er;

Det første og andre argumentet for funksjonen eren enkel matrise, ettersom det tar matrise som argument, vil vi legge plasseringen av cellen der matrisen er bosatt. Du kan imidlertid også sette inn verdier direkte.

Vi vil skrive denne funksjonen som;

Som A2:B3 er plasseringen av cellen der den første matrisen vår er bosatt, og E2: F3 er stedet for den andre. Som vi har hatt med å gjøre her, så må du trykke på Ctrl + Shift + Enter for å omslutte funksjonen i krøllete parenteser, som indikerer bruken av matriser.

Velg nå de første matrikscellene i multiplikasjon og bare gå inn i funksjonen som nevnt over. Det vil gi multiplikasjonsresultatet i 4 celler da vi har evaluert 2 × 2 matrise.

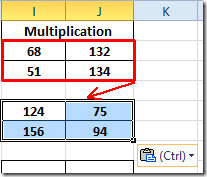
For å finne ut multiplikasjonsresultater i andrematriser, velg den evaluerte matrisen og bare kopier og lim inn i andre 2 × 2 matriser. Som vist nedenfor, at vi nettopp har kopiert matrisen til matrise under den.

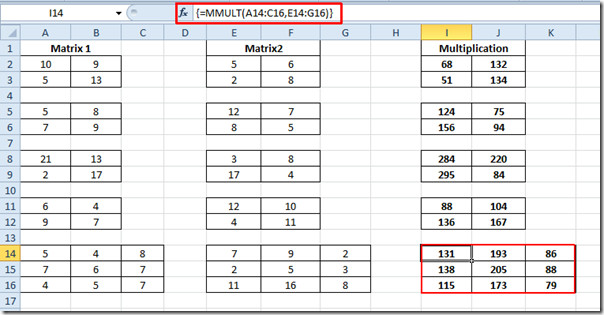
Gjenta nå samme prosedyre for alle 2 × 2 matriser. For 3 × 3-matrise, skriv ned funksjonen igjen ved å oppgi hver celleplassering i begge matriser.

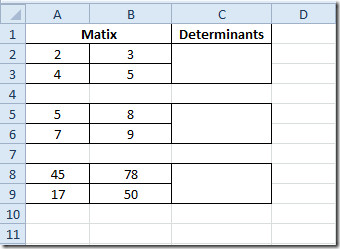
Du kan også sjekke ut tidligere gjennomgåtte Matrix-driftsfunksjon; Evaluering av Matrix Determinant (MDETERM) og finne ut Inverse of Matrix.