Înmulțirea matricei Excel 2010 (MMULT)

Anterior am abordat modul de evaluare a inversului matricei. Acum vom folosi Excelent inerent MMULT funcție pentru a afla înmulțirea directă a matricei, mai degrabă decât a merge la formularea manuală. De asemenea, tratează valorile datelor ca matrice și ia matricea ca argument (e).

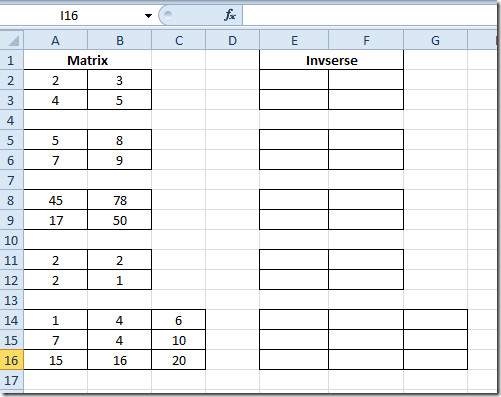
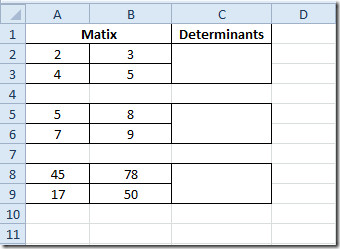
Lansați o foaie de calcul Excel 2010 pe care trebuie să aflați înmulțirea matricei. De exemplu, am inclus o foaie de calcul care conține câmpuri; Matrix1, Matrix2 și Multiplicare așa cum se arată în imaginea de mai jos.

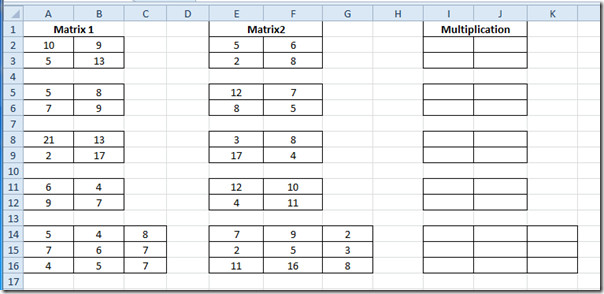
Vom afla multiplicareamatrici. Avem trei matrice 2 × 2 și una 3 × 3. Formula ar fi absolut aceeași pentru fiecare categorie. Vechea metodă de evaluare a înmulțirii ar putea fi foarte lungă mai ales atunci când avem de-a face cu matricea 3 × 3. Vom folosi însă funcția MMULT Sintaxa de bază a acestor funcții este;

Primul și al doilea argument al funcției esteo matrice simplă, întrucât are argumentul ca argument, vom pune locația celulei în care rezidă matricea. Cu toate acestea, puteți pune și valori direct.

Vom scrie această funcție ca;

Ca A2:B3 este locația celulei în care rezidă prima noastră matrice și E2: F3 este locația celei de-a doua. Așa cum am avut de-a face cu matricea aici, trebuie să apăsați Ctrl + Shift + Enter pentru a închide funcția în paranteze cret, ceea ce indică utilizarea tablelor.

Acum selectați primele celule matrice din Multiplicare câmp și trebuie doar să introduceți funcția așa cum am menționat mai sus. Va rezulta rezultatul înmulțirii în 4 celule, după cum am evaluat matricea 2 × 2.

Pentru aflarea rezultatelor înmulțirii în altelematricile, selectați matricea evaluată și copiați și inserați-le în alte matrici 2 × 2. Așa cum este arătat mai jos, tocmai am copiat matricea în matrice sub ea.

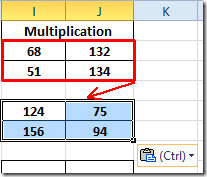
Acum repetați aceeași procedură pentru toate matricile 2 × 2. Pentru matrice 3 × 3, notează din nou funcția, furnizând fiecare locație a celulelor în ambele matrice.

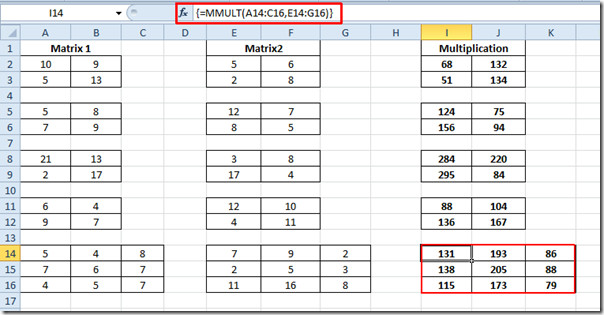
Puteți verifica, de asemenea, funcția de operare Matrix revizuită anterior; Evaluarea determinării matricei (MDETERM) și descoperirea inversă a matricei.