Daha önce, matrisin tersinin nasıl değerlendirileceğini ele aldık. Şimdi Excel'in doğasında kullanacağız MMULT manuel formülasyonu kullanmak yerine doğrudan matrisin çarpımını bulma işlevi. Ayrıca dizi olarak veri değerleriyle ilgilenir ve diziyi argüman (lar) olarak alır.
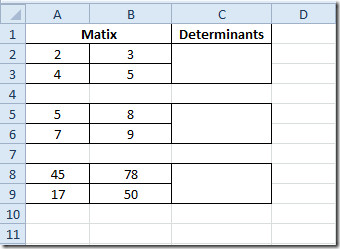
Matris çarpımını bulmanız gereken Excel 2010 elektronik tablosunu başlatın. Örneğin, alanları içeren bir elektronik tablo ekledik; Matrix1, Matrix2 ve Çarpma işlemi Aşağıdaki ekran görüntüsünde gösterildiği gibi.
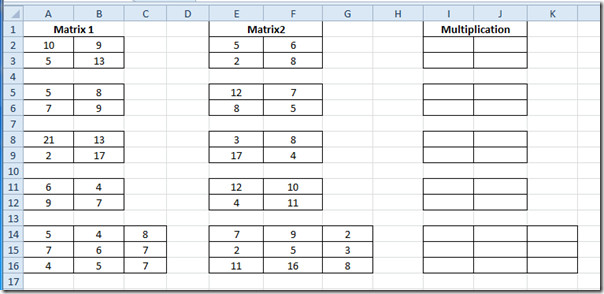
Çarpımını bulacağızmatrisler. Üç 2 x 2 ve bir 3 x 3 matrisimiz var. Formül, her kategori için kesinlikle aynı olacaktır. Eski çarpımı değerlendirme yöntemi, özellikle 3 x 3 matrisle başa çıkmamız gerektiğinde çok uzun olabilir. Ancak MMULT işlevini kullanacağız. Bu işlevlerin temel sözdizimi;
= MMULT (array1, array2)
Fonksiyonun birinci ve ikinci argümanıbasit bir dizi, diziyi argüman olarak alır, dizinin bulunduğu hücrenin konumunu koyacağız. Bununla birlikte, doğrudan değerleri de girebilirsiniz.
Bu işlevi şöyle yazacağız;
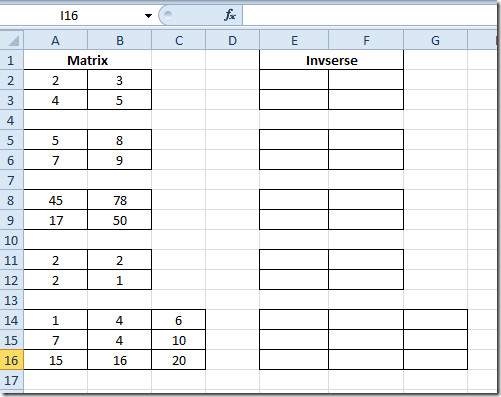
{= MMULT (A2: B3, E2: F3)}
A2 olarak:B3, ilk matrisimizin bulunduğu hücrenin yeri ve E2: F3 ikincisinin yeridir. Buradaki dizi ile ilgilendiğimiz için, dizilerin kullanımını gösteren, işlevi parantez içindeki parantez içine almak için Ctrl + Shift + Enter tuşlarına basmanız gerekir.
Şimdi ilk matris hücrelerini seçin. Çarpma işlemi alan ve sadece yukarıda belirtildiği gibi işlevi girin. 2 × 2 matrisi değerlendirdiğimiz için 4 hücrede çarpma sonucunu verecektir.
![mutiplication]](/images/ms-office/excel-2010-matrix-multiplication-mmult_2.jpg)
Diğer çarpma sonuçlarını bulmak içinmatrisleri, değerlendirilen matrisi seçin ve diğer 2 × 2 matrislere kopyalayıp yapıştırın. Aşağıda gösterildiği gibi, matrisi henüz altındaki matrise kopyaladık.
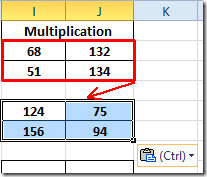
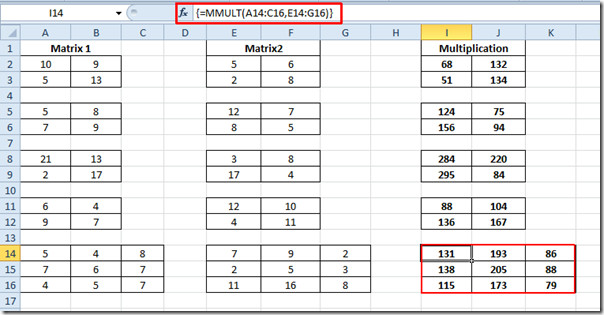
Şimdi tüm 2 × 2 matrisler için aynı işlemi tekrarlayın. 3 × 3 matriks için, her iki matristeki her hücre konumunu sağlayarak fonksiyonu tekrar yazın.
{= MMULT (A14: C16, E14: G16)}
Ayrıca daha önce gözden geçirilmiş Matris işlemi İşlevine bakabilirsiniz; Matris Belirleyicisinin (MDETERM) Değerlendirilmesi ve Matrisin Tersinin Bulunması.








Yorumlar