Матричне множення Excel 2010 (MMULT)

Раніше ми розглядали, як оцінити оберненість матриці. Зараз ми будемо використовувати притаманні Excel MMULT функція безпосередньо знаходити множення матриці, а не переходити до ручного формулювання. Він також має справу зі значеннями даних як масив і приймає масив як аргументи.

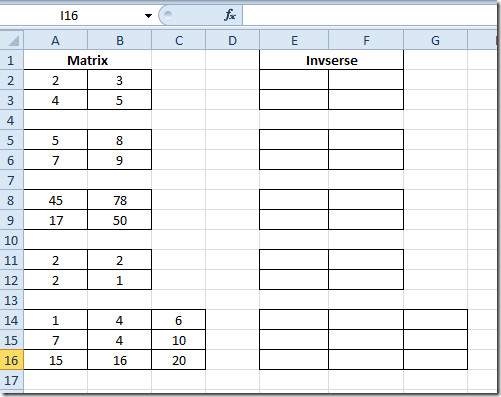
Запустіть таблицю Excel 2010, на якій потрібно дізнатися множення матриць. Наприклад, ми включили таблицю, що містить поля; Матриця1, Матриця2 і Множення як показано на скріншоті нижче.

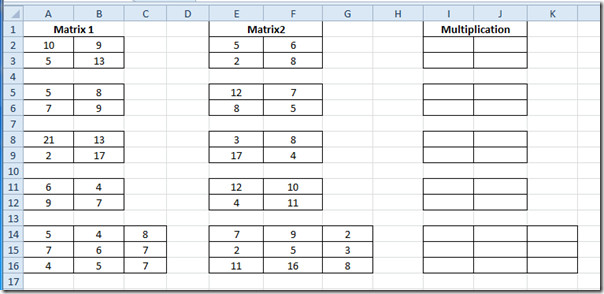
Ми з’ясуємо множення числаматриці. Маємо три матриці 2 × 2 та одну матрицю 3 × 3. Формула була б абсолютно однаковою для кожної категорії. Старий метод оцінювання множення може бути дуже тривалим, особливо коли ми маємо справу з матрицею 3 × 3. Але ми будемо використовувати функцію MMULT Основний синтаксис цієї функції:

Перший і другий аргумент функціїпростий масив, оскільки він приймає масив як аргумент, ми будемо розміщувати розташування комірки, де мешкає масив. Однак ви також можете вводити значення безпосередньо.

Цю функцію ми запишемо як;

Як A2:B3 - це розташування комірки, де проживає наша перша матриця, а E2: F3 - розташування другої. Оскільки тут ми маємо справу з масивом, тому вам потрібно натиснути Ctrl + Shift + Enter, щоб укласти функцію у фігурні дужки, що вказує на використання масивів.

Тепер виберіть перші клітини матриці в Множення поле та просто введіть функцію, як було сказано вище. Це дасть результат множення в 4 клітинках, як ми оцінювали матрицю 2 × 2.

Для з’ясування результатів множення в іншихматриць, виберіть оцінювану матрицю та просто скопіюйте та вставте в інші 2 × 2 матриці. Як показано нижче, ми щойно скопіювали матрицю в матрицю під нею.

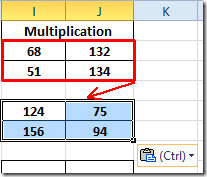
Тепер повторіть ту ж процедуру для всіх матриць 2 × 2. Для матриці 3 × 3 запишіть функцію ще раз, вказавши місце розташування кожної комірки в обох матрицях.

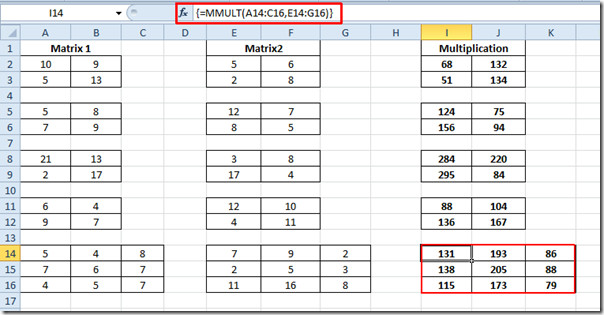
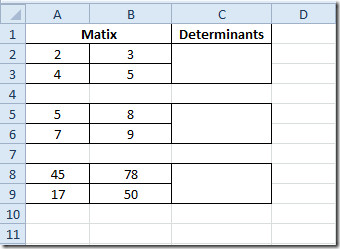
Ви також можете перевірити раніше переглянуту функцію роботи матриці; Оцінка детермінанта матриці (MDETERM) та виявлення зворотної матриці.