Раније смо описали како то оценитиодредница матрице. Сада ћемо се фокусирати на то како сазнати обрнуту матрицу која углавном захтева множење детерминанти са ад-спојом матрице. Метода старе школе за процену обрнутог је веома заморна, али са Екцелом МИНВЕРСЕ функцију, можемо је процијенити одмах. Треба само да напишемо или одредимо вредности распона података у матрици као аргумент функције.
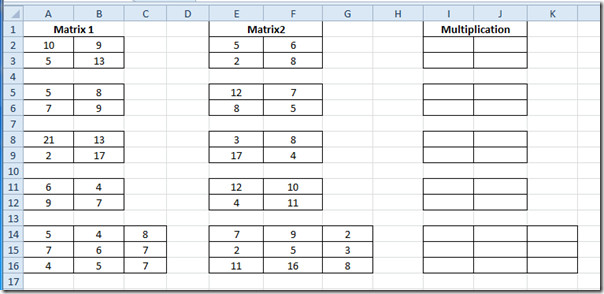
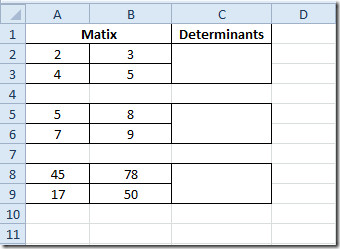
Покрените прорачунску таблицу Екцел 2010 која садржи податке у матрицама. На пример, укључили смо табелу која садржи поља; Матрица и Инверзно.
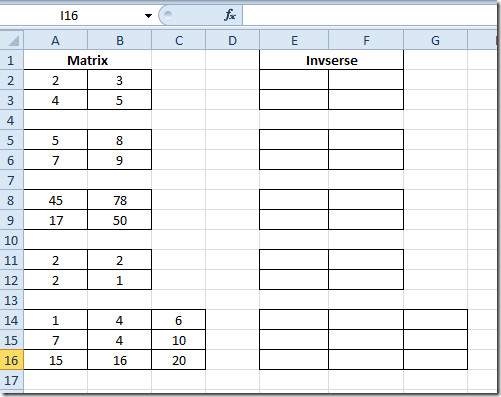
Као што сте приметили да постоје три 2 × 2матрице и једна матрица 3 × 3, ми ћемо сазнати обрнуто матрике помоћу Екцел-ове инхерентне функције, а не да применимо олд-сцхоол метод за процену инверзије матрице која је;
Инверзно (А) = | А | Матрица (Адј [А])
Сигурно сте били упознати са процесом евалуације, постаје толико сложен и напоран за управљање. Али ми ћемо користити МИНВЕРСЕ функција која ће одмах добити инверзију матрице.
Основна синтакса функције је;
= МИНВЕРСЕ (низ)
Где поље може бити распон података или вредности унесене у облику низа. Формулу ћемо писати у првој матрици у Инверзно колона.
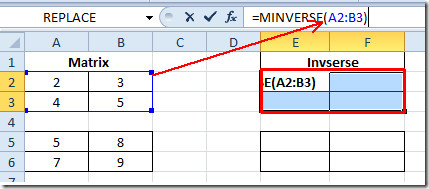
= МИНВЕРСЕ (А2: Б3)
Где је А2: Б3 распон података матрице у Матрица поље. Изаберите прву матрицу у Инверзно поље тј Е2: Ф3. и напишите формулу као што је горе поменуто.
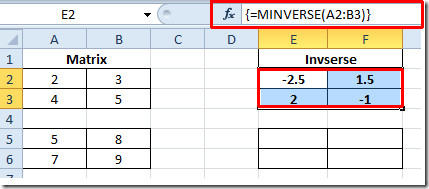
Сада притисните Цтрл + Схифт + Ентер на тастатури да бисте Екцел-у знали да имамо посла са низом. Формула ће бити затворена у заградама { = МИНВЕРСЕ (А2: Б3) }, као што је приказано на слици испод.
Примените формулу копирањем и лепљењем у друге ћелије након што одаберете ћелије које садрже другу матрицу.
За матрицу 3 × 3 поново ћемо записати формулу, изабрати ћелије које садрже у матрици и формула ће ићи овако;
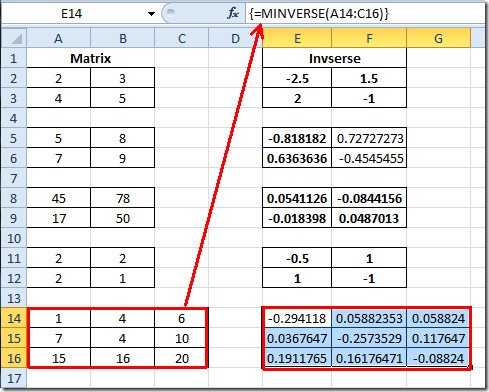
{= МИНВЕРСЕ (А14: Ц16)}
Даје резултат обрнутог матрикса у одабраним ћелијама, као што је приказано на слици испод.
Такођер можете провјерити претходно прегледани рад матрице Функција оцјењивања детерџента матрице (МДЕТЕРМ) и друге функције; ДОЛЛАР, СУМПРОДУЦТ, СУМИФ, ЦОУНТИФ, ВЛООКУП, ХЛООКУП, ПМТ и ЛЕН.







Коментари