Екцел 2010 Матрик множење (ММУЛТ)

Раније смо описали како оценити инверзију матрице. Сада ћемо користити својство Екцел-а ММУЛТ функција за проналажење множења матрице директно, а не за ручно формулисање. Такође се бави вриједностима података као низ и узима низ као аргументе.

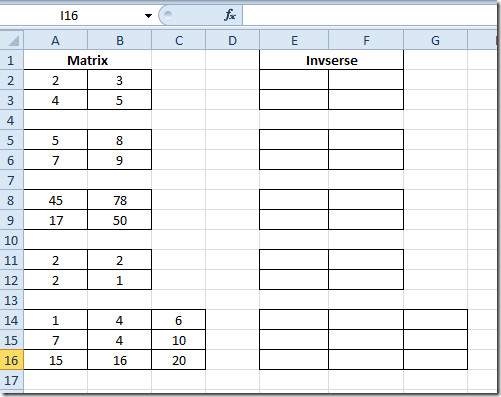
Покрените прорачунску таблицу Екцел 2010 на којој морате сазнати множење матрице. На пример, укључили смо прорачунску табелу која садржи поља; Матрик1, Матрик2 и Умножавање као што је приказано на слици испод.

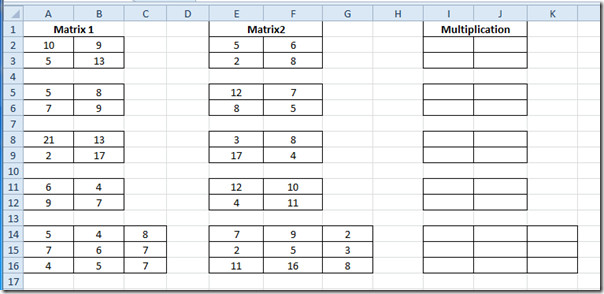
Открићемо множењематрице. Имамо три матрице 2 × 2 и једну матрицу 3 × 3. Формула би била апсолутно иста за сваку категорију. Стара метода процене множења могла би бити веома дугачка, посебно када морамо да се позабавимо матрицом 3 × 3. Али ми ћемо користити функцију ММУЛТ. Основна синтакса ове функције је;

Први и други аргумент функције јеједноставна матрица, јер узима арраи као аргумент, ми ћемо постављати локацију ћелије у којој низ пребива. Међутим, такође можете директно уносити вредности.

Ову функцију ћемо написати као;

Као А2:Б3 је локација ћелије у којој борави наша прва матрица, а Е2: Ф3 је локација друге. Као што се овде бавимо низом, тако да морате притиснути Цтрл + Схифт + Ентер да бисте функцију закључали у коврчавим заградама, што указује на употребу низова.

Сада одаберите прве матричне ћелије у Умножавање поље и само унесите функцију како је горе поменуто. Добиће резултат множења у 4 ћелије, као што смо оцењивали матрицу 2 × 2.

За проналажење резултата множења у другимматрице, одаберите процењену матрицу и само копирајте и залепите у друге 2 × 2 матрице. Као што је приказано у даљем тексту, управо смо копирали матрицу у матрицу испод ње.

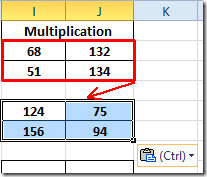
Сада поновите исти поступак за све 2 × 2 матрице. За матрицу 3 × 3, поново запишите функцију тако што ћете обе локације додати у обе матрице.

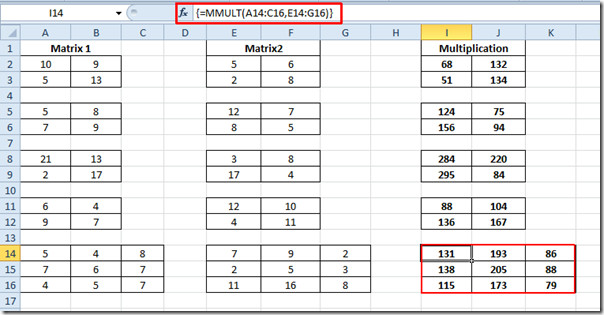
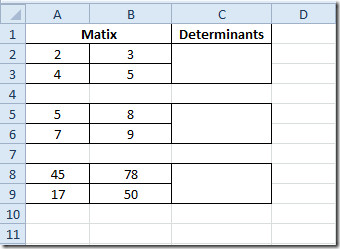
Такође можете проверити претходно прегледану функцију рада матрице; Процена детерминанти матрице (МДЕТЕРМ) и откривање обрнутости матрице.